Rooks Problem -- from Wolfram MathWorld
Por um escritor misterioso
Last updated 16 junho 2024

The rook is a chess piece that may move any number of spaces either horizontally or vertically per move. The maximum number of nonattacking rooks that may be placed on an n×n chessboard is n. This arrangement is achieved by placing the rooks along the diagonal (Madachy 1979). The total number of ways of placing n nonattacking rooks on an n×n board is n! (Madachy 1979, p. 47). In general, the polynomial R_(mn)(x)=sum_(k)r_k^((m,n))x^k whose coefficients r_k^((m,n)) give the

N-Queen's Puzzle – ChristianSabdana

Rook Polynomials: A Straight-Forward Problem – Feature Column
TrackStar

How 8 Queens Works

Aggregation and Tiling as Multicomputational Processes—Stephen Wolfram Writings

Rook polynomial - Wikipedia

Using Wolfram, Alpha to Understand Mathematics

Rook Polynomial -- from Wolfram MathWorld

Laguerre polynomials - Wikipedia

Rook Polynomial -- from Wolfram MathWorld

Rook Polynomials: A Straight-Forward Problem – Feature Column
Recomendado para você
-
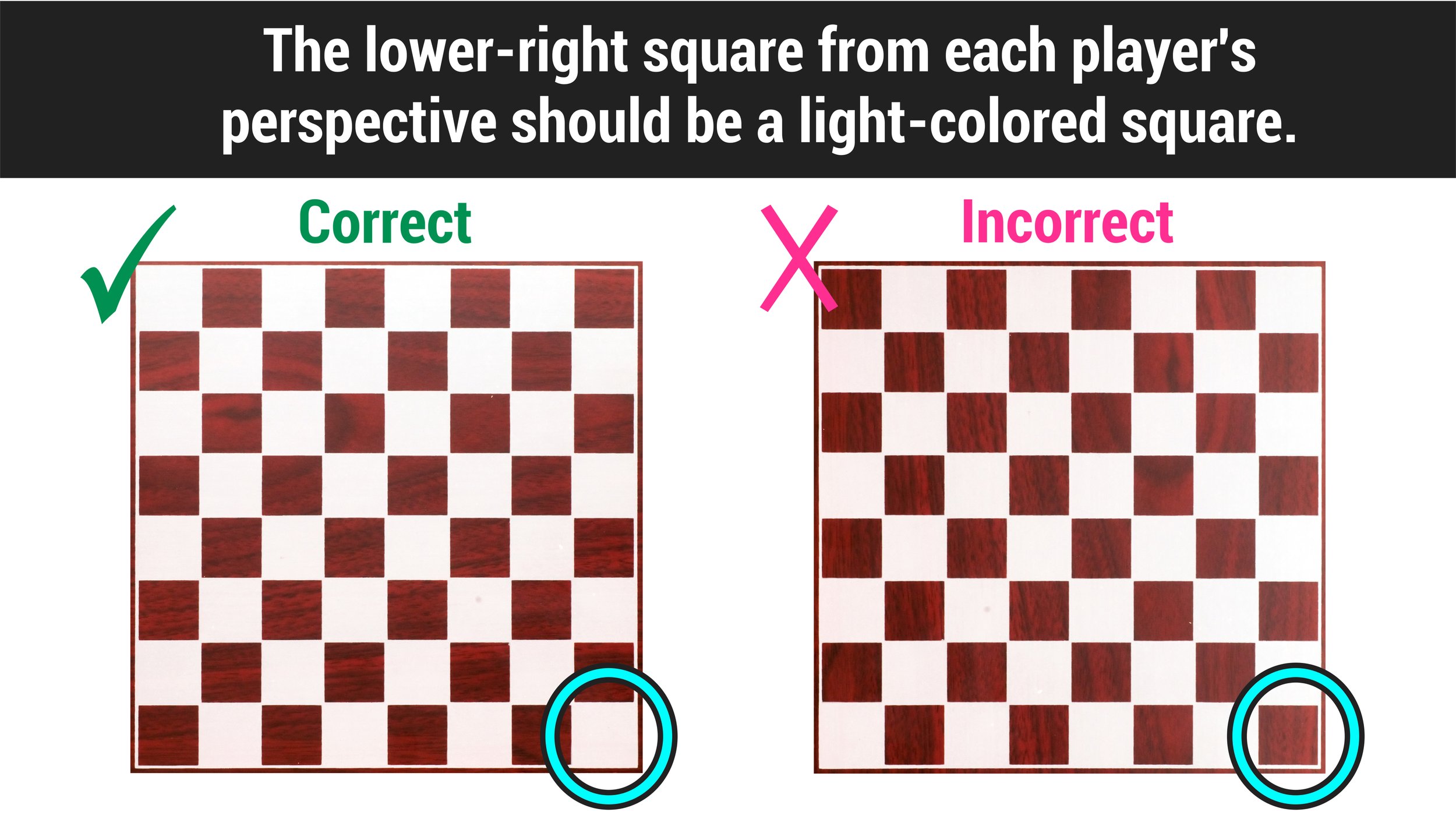 How to Set Up a Chess Board—Explained — Mashup Math16 junho 2024
How to Set Up a Chess Board—Explained — Mashup Math16 junho 2024 -
Chess Recognition Problem: A Deep Dive Solution16 junho 2024
-
 Chess Puzzles - Rook Strategies16 junho 2024
Chess Puzzles - Rook Strategies16 junho 2024 -
Chess Rooks Problem - Apps on Google Play16 junho 2024
-
 Forget 3-D Chess; Here's My 1-D Chess Rules16 junho 2024
Forget 3-D Chess; Here's My 1-D Chess Rules16 junho 2024 -
To place 8 rooks on the chessboard16 junho 2024
-
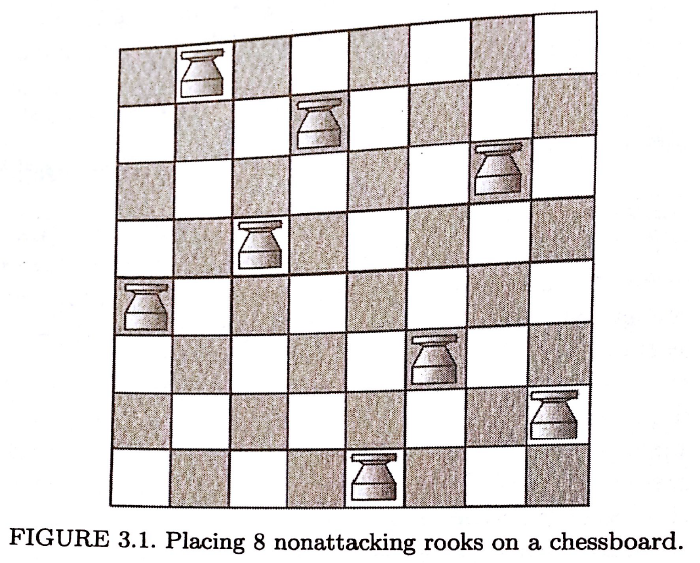 Solved Figure 3.1 Placing 8 nonattacking rooks on a16 junho 2024
Solved Figure 3.1 Placing 8 nonattacking rooks on a16 junho 2024 -
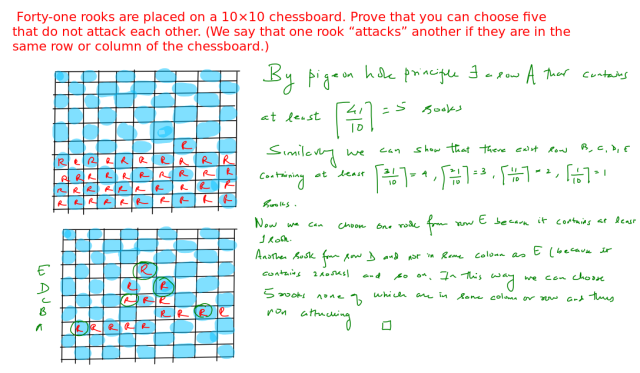 Choosing 5 non attacking rooks out of 41 rooks on a 10 by 10 chess board16 junho 2024
Choosing 5 non attacking rooks out of 41 rooks on a 10 by 10 chess board16 junho 2024 -
 Enemy rooks are connected? No problem! Black to move : r/chess16 junho 2024
Enemy rooks are connected? No problem! Black to move : r/chess16 junho 2024 -
 CHAPTER 4 OTHER FORKS/DOUBLE ATTACKS Diagram 124 - White wins a Rook or Knight in 2 moves.16 junho 2024
CHAPTER 4 OTHER FORKS/DOUBLE ATTACKS Diagram 124 - White wins a Rook or Knight in 2 moves.16 junho 2024
você pode gostar
-
 Review: Infinite Stratos The Tiny World of an Anime Amateur16 junho 2024
Review: Infinite Stratos The Tiny World of an Anime Amateur16 junho 2024 -
 10 crossovers de desenhos animados que a gente esqueceu que existiu16 junho 2024
10 crossovers de desenhos animados que a gente esqueceu que existiu16 junho 2024 -
 Sailor Moon Cosmos Anime Films Showcase Usagi's Eternal Transformation - Crunchyroll News16 junho 2024
Sailor Moon Cosmos Anime Films Showcase Usagi's Eternal Transformation - Crunchyroll News16 junho 2024 -
 File:The dead end.jpg - Wikimedia Commons16 junho 2024
File:The dead end.jpg - Wikimedia Commons16 junho 2024 -
 JJBA Fan-Stands: Wonderwall by SRegan on DeviantArt16 junho 2024
JJBA Fan-Stands: Wonderwall by SRegan on DeviantArt16 junho 2024 -
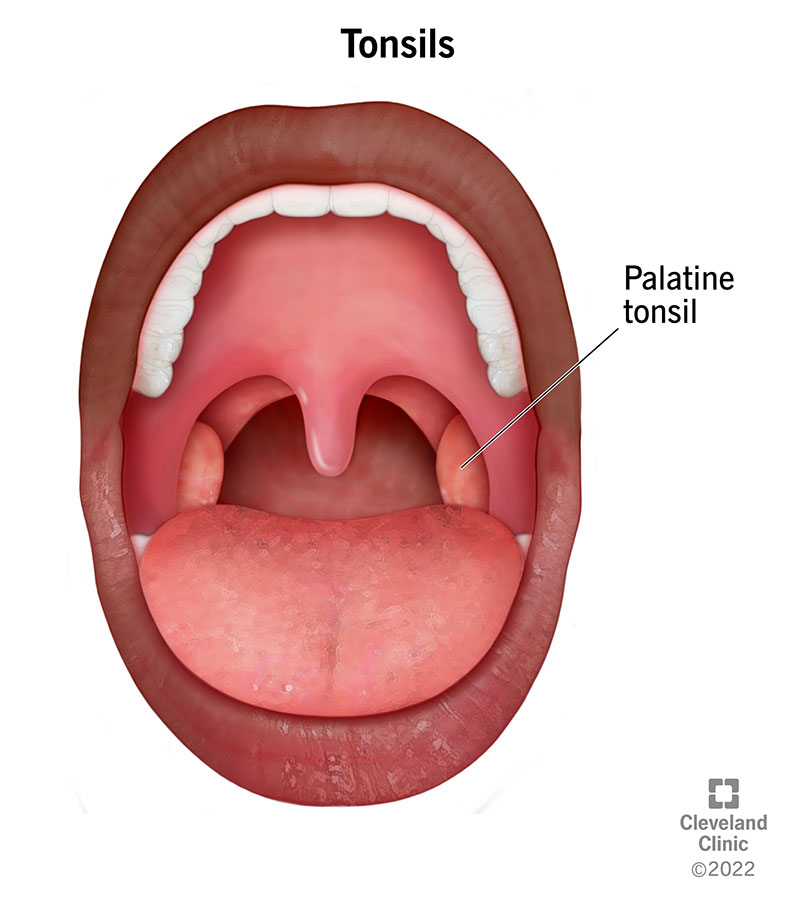
Tonsils: Anatomy, Definition & Function16 junho 2024
-
 Dragon Age: Origins Free on Origin - IGN16 junho 2024
Dragon Age: Origins Free on Origin - IGN16 junho 2024 -
 Especial Animes: Berserk Era de Ouro Ato II - A Batalha de Doldrey16 junho 2024
Especial Animes: Berserk Era de Ouro Ato II - A Batalha de Doldrey16 junho 2024 -
 A Realidade Do Mundo À Luz Dos Documentos Da Igreja by Nilso Schneider16 junho 2024
A Realidade Do Mundo À Luz Dos Documentos Da Igreja by Nilso Schneider16 junho 2024 -
Intended as the B-side for “Love Song,” “Baby Please Don't Go” became , acdc16 junho 2024