1) Sketch the parabola, and lable the focus, vertex and directrix. a) (y - 1)^2 = -12(x + 4) b) i) y^2 - 6y -2x + 1 = 0, ii) y =
Por um escritor misterioso
Last updated 16 junho 2024


Day 18 Warm-Up 1) Which of the following problems is a circle and which is a parabola? Why? A) ppt download

1 Lactus Rectum, PDF, Mathematical Objects

Find the vertex, focus, and directrix of each parabola. Grap
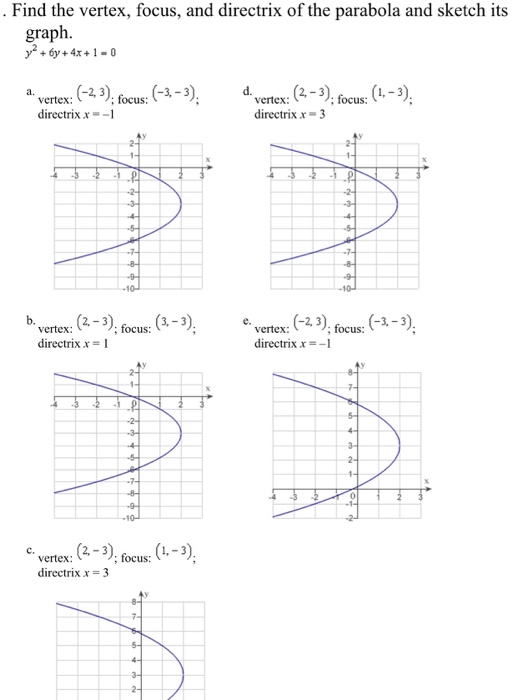
Solved Find the vertex, focus, and directrix of the parabola

Answered: Identify the directrix, focus, and…

Pre-Calculus Prep: Conic Sections - Graph the Ellipse

Find a polar equation of the conic with its focus at the pole. Parabola; (8, 0)

HELP! ONLY IF YOU KNOW THE ANSWER also this goes with the other question I asked Write the standard

geometry - Focus of parabola with two tangents - Mathematics Stack Exchange
Recomendado para você
-
 DirectX 12 (Ultimate) Download for Windows 10/11 PC - MiniTool16 junho 2024
DirectX 12 (Ultimate) Download for Windows 10/11 PC - MiniTool16 junho 2024 -
 DirectX 12 - Download for PC Free16 junho 2024
DirectX 12 - Download for PC Free16 junho 2024 -
Using DeviceResources · microsoft/DirectXTK12 Wiki · GitHub16 junho 2024
-
 AMD DirectX® 12 (DX12) Technology16 junho 2024
AMD DirectX® 12 (DX12) Technology16 junho 2024 -
 DirectX 12 Will Allow Multi-GPU Between GeForce And Radeon : r/Games16 junho 2024
DirectX 12 Will Allow Multi-GPU Between GeForce And Radeon : r/Games16 junho 2024 -
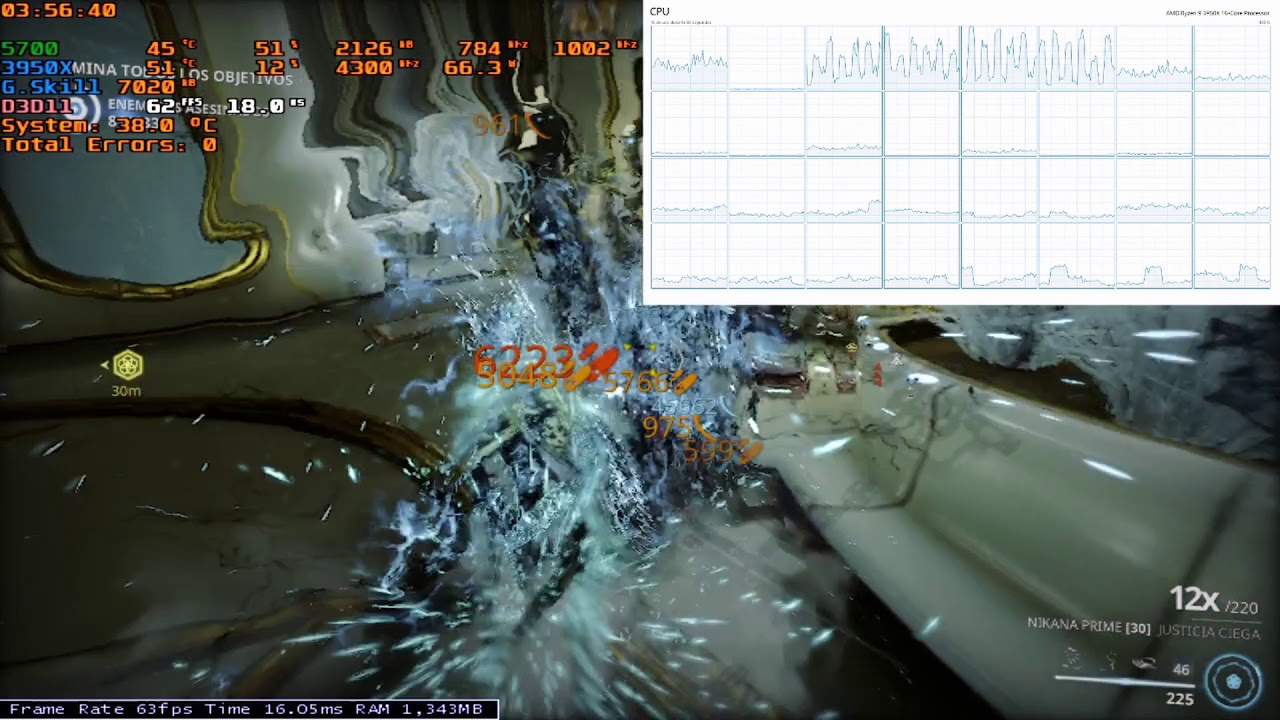 Warframe DX11 vs DX12 Round 2 Update 29.6.3 (no GPU bound)16 junho 2024
Warframe DX11 vs DX12 Round 2 Update 29.6.3 (no GPU bound)16 junho 2024 -
 Fortnite: Chapter 3 Season 2 - DirectX 11 vs DirectX 12 vs Performance Mode - FPS Boost16 junho 2024
Fortnite: Chapter 3 Season 2 - DirectX 11 vs DirectX 12 vs Performance Mode - FPS Boost16 junho 2024 -
 All NEW Fortnite Chapter 2 Settings! - DirectX 12, Console Motion Blur, & More!16 junho 2024
All NEW Fortnite Chapter 2 Settings! - DirectX 12, Console Motion Blur, & More!16 junho 2024 -
 NVIDIA Ion Reference PC Platform Deep Dive16 junho 2024
NVIDIA Ion Reference PC Platform Deep Dive16 junho 2024 -
 Dungeon Lords review16 junho 2024
Dungeon Lords review16 junho 2024
você pode gostar
-
 Street Fighter 6 PC Requirements: Minimum & recommended specs - Dexerto16 junho 2024
Street Fighter 6 PC Requirements: Minimum & recommended specs - Dexerto16 junho 2024 -
 Gaolang Wongsawat VS Ricardo Martinez from Hajime No Ippo who wins in a boxing match? : r/Kengan_Ashura16 junho 2024
Gaolang Wongsawat VS Ricardo Martinez from Hajime No Ippo who wins in a boxing match? : r/Kengan_Ashura16 junho 2024 -
 Baldur's Gate 3: Necromancy Of Thay Location & Choice Guide16 junho 2024
Baldur's Gate 3: Necromancy Of Thay Location & Choice Guide16 junho 2024 -
Ho-Oh Shiny Brilhante Pokemon Go (30 Dias de Amizade)16 junho 2024
-
 Realistic Summer Mansion Bloxburg Speedbuild16 junho 2024
Realistic Summer Mansion Bloxburg Speedbuild16 junho 2024 -
 EVS Sports Black Epic CE Knee Pads - Dennis Kirk16 junho 2024
EVS Sports Black Epic CE Knee Pads - Dennis Kirk16 junho 2024 -
 Como baixar e instalar um app fora da play store no Samsung A12 - Passo a passo16 junho 2024
Como baixar e instalar um app fora da play store no Samsung A12 - Passo a passo16 junho 2024 -
![Spider-Man: Otto Octavius / Doc Ock [INFJ 3w2] – Funky MBTI](https://funkymbti.files.wordpress.com/2021/01/ock.jpg) Spider-Man: Otto Octavius / Doc Ock [INFJ 3w2] – Funky MBTI16 junho 2024
Spider-Man: Otto Octavius / Doc Ock [INFJ 3w2] – Funky MBTI16 junho 2024 -
![Jailbreak] Can no longer rob the Cargo Ship with Ropes in Public](https://devforum-uploads.s3.dualstack.us-east-2.amazonaws.com/uploads/original/4X/b/d/0/bd02308345b4930011489b7d86292b5915a761b2.jpeg) Jailbreak] Can no longer rob the Cargo Ship with Ropes in Public16 junho 2024
Jailbreak] Can no longer rob the Cargo Ship with Ropes in Public16 junho 2024 -
Hand Simulator System Requirements: Can You Run It?16 junho 2024